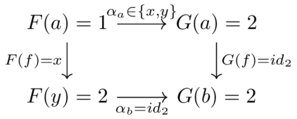Exercise 3-58

Let \(\mathcal{C}\) be an arbitrary category and \(\mathcal{P}\) be a preorder thought of as a category. Are the following true?

  1. For any two functors \(\mathcal{C}\xrightarrow{F,G}\mathcal{P}\), there is at most one natural transformation \(F \rightarrow G\)

  2. For any two functors \(\mathcal{P}\xrightarrow{F,G}\mathcal{C}\), there is at most one natural transformation \(F \rightarrow G\)

Solution(1)

  1. This is true: there are no choices to be made for a natural transformation, given that for each morphism \(c\rightarrow d\) in \(\mathcal{C}\) we have to pick \(\alpha_c\) to be the morphism \(F(c)\rightarrow G(c)\) and \(\alpha_{d}\) to be the morphism \(F(d)\rightarrow G(d)\).

  2. Counterexample:

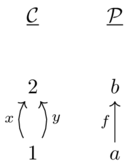
    • let \(F\) send \(f\mapsto x,a\mapsto1,b\mapsto 2\) and \(G\) maps everything to \(2\)

    • The naturality condition for f leaves us with two choices for \(\alpha_a\)